Proland Documentation - River Plugin
The river plugin is based on the paper "Scalable Real-Time Animation of Rivers", Qizhi Yu, Fabrice Neyret, Eric Bruneton and Nicolas Holzschuch, Eurographics 2009. It allows to render in real-time animated rivers based on graphs and on a particle system. This plugin requires the terrain and the graph plugins.

We recall here the main principles of the above algorithm (the details can be found in the article):
- the rendering of the river surface is done with a set of sprites. Each sprite is textured with a small wave tile representing characteristic river surface features. These sprites are blended together during rendering to give a continuous river surface with waves.
- the animation of the river surface comes from two things. First, the wave tile textures are animated. Thus surface waves are animated even if the water is not flowing (for instance in lakes). Second, and most importantly, the sprites are attached to particles that are advected with the river flow. This means that each sprite is centered on a particle, and that particle positions are updated at each frame based on the velocity field of the river.
The scalability of the algorithm comes from two important features:
- first, particles do not cover the whole river surface, but only the parts that are visible at a given time. Also distant parts are covered with less, bigger particles than parts that are close to the camera. This ensures that the amount of particles (which directly impacts performance since the animation and rendering steps costs are directly proportional to this number) stays bounded, even if the river network is very large. These properties are ensured by managing particles almost entirely in screen space. In particular, a particle producer keeps the size and the density of particles constant in screen space. This automatically ensures that only visible river parts are covered, with bigger particles (in world space) for more distant parts. World space computations are only used to advect the particles.
- the second feature that gives a scalable algorithm is the method used to compute the velocity field of the river (used itself for advecting the particles in world space). Instead of using Computational Fluid Dynamics methods, which require costly simulations on the whole river network, Qizhi Yu's algorithm uses a procedural velocity field which can be computed at each point independently of others, based only on the distance between this point and the nearby river banks (within a disc of bounded radius, in world space), as well as the value of a stream function along these banks (this stream function is also called the potential since the velocity field is computed from the derivatives of this function).
The proland module is divided in several parts corresponding to logical steps in the above algorithm. Going from the inputs to the outputs of the algorithm, these parts are the following (they are described in more details in the following sections):
- the graph framework provides classes to describe the inputs of the algorithm, namely the river network. This network is a graph made of curves describing the river banks. The graph framework can describe graphs and curves, but it cannot associate to each curve the stream function value, also called a potential, required by the rivers algorithm (as explained above). For this an extension of the graph framework is provided in the graph module, which adds all necessary data to curves to describe river networks.
- the proland::HydroFlowProducer and proland::HydroFlowTile classes implement the procedural velocity field algorithm, using as input a river network described with a river graph.
- the proland::particles framework provides classes to manage particles in screen space, and in particular to keep a constant particle density in screen space. The classes of this framework are also responsible to compute the initial world space position of new particles. These initial world space positions are then advected with the velocity field computed by the proland::HydroFlowProducer.
- Finally the remaining classes of rivers are responsible to draw and blend sprites associated with the previous particles, and textured with animated wave tiles, in order to render an animated river surface.
These four parts and the relations between them are illustrated by the following UML diagram:
The river networks used as input by the rivers module are called hydro graphs. It is important to note here that our representation of hydro graphs is not exactly the same as in Qizhi Yu's paper. In this paper, only rivers banks and obstacles are explicitely represented. In our representation, we also require an explicit representation of the river axis: this must be a curve corresponding roughly to the river central axis, whose width must be large enough to cover the river banks. Another difference is that we require each river bank to have a reference to the corresponding river axis (in addition to the stream function value on this bank, as in Qizhi Yu's paper).
The river axis curves are necessary for the proland::WaterElevationLayer (to flatten the terrain in order to get a correct river bed). They are also usefull in the rivers module as a quick test to check if a particle may be inside a river (see next section). The references between the river banks and the river axis are needed by our implementation of the procedural velocity field algorithm (see next section).
The next figure shows how an hydro graph must be organized.
Implementation
The graph framework is not sufficient to describe river networks. It is therefore extended in river graph to allow the description of these networks, called hydro graphs.
Hydro graphs are represented by proland::HydroGraph and proland::LazyHydroGraph. These are subclasses of proland::BasicGraph and proland::LazyGraph, respectively. The main difference with a classic graph is that we needed two more information for each river bank: a flow potential and a reference to the river axis curve. This new information is stored in proland::HydroCurve (and proland::LazyHydroCurve).
Then, the proland::HydroGraph extends proland::BasicGraph only to create HydroCurve instead of BasicCurve, and to load from and save to files the additional data of each hydro curve. In these files each curve must now have 5 parameters, instead of 3 for basic graphs. The two new parameters must be placed after the 3 default ones (size, width and type):
- number of vertices (including the start and end nodes - integer).
- width (float).
- type (integer).
- potential value (float).
- identifier of the corresponding river axis curve (-1 if the curve is not a river bank) (integer).
Note that these files remains compatible with other graphs. The river data will just be ignored if a river graph is used where a regular graph was expected. The river algorithm is mainly based on the curves' type, so it is necessary to correctly set this value for every curve: The HydroCurve::AXIS value can be used for river axis that you want to be displayed. Generally, it is best to put the river axis Curve's type to HydroCurve::CLOSING_SEGMENT. That type is used for non-displayed Curves, and can be linked to. They may be used to close banks at river ends, in order to form a loop. Finally, HydroCurve::BANK should be used to create banks or obstacles (islands, moving items in water...). Curves with this type must have a defined potential value.
Algorithm
The figure below recalls the principles of Qizhi Yu's algorithm to compute the velocity field inside rivers in a procedural way (see the paper for details):
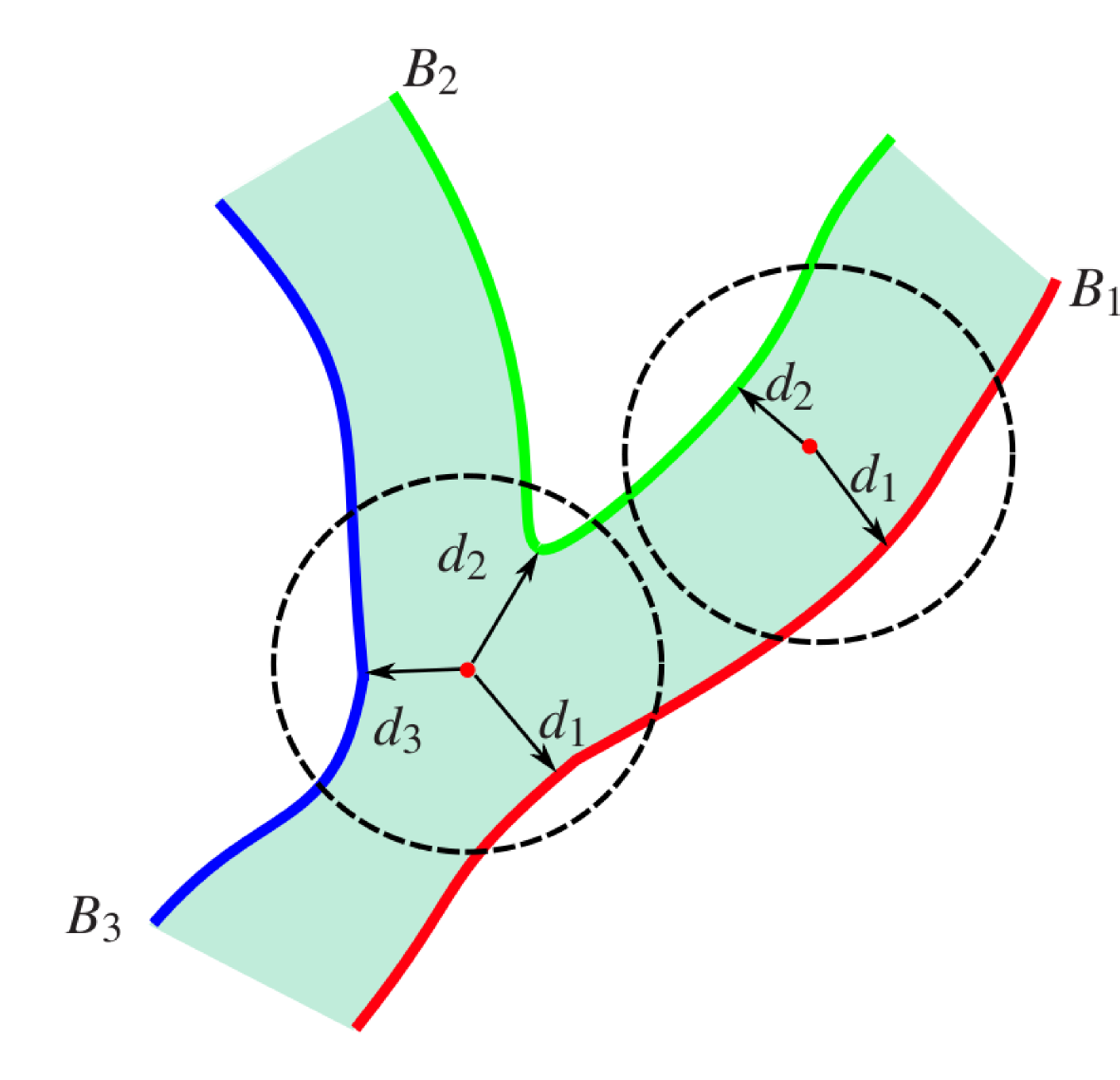
Our implementation of this algorithm is a little bit different from the one described in Qizhi Yu's paper. Indeed we make use of an additional data associated with each river bank curve: a link to the corresponding river axis curve (see previous section).
As in Qizhi Yu's paper, this basic algorithm is improved by using an acceleration data structure to quickly find the river banks that lie within a finite distance of a given point. This data structure is not computed for the whole river graph once and for all, in order to allow real-time river graph editing. Instead, it is computed on the fly for each river graph tile produced by the tile producer framework (i.e. when new tiles comes into view). It is recomputed each time the river graph is edited.
This acceleration data structure contains a simplified version of the river graph, and only references the curves that are large enough to be displayed on screen (based on a tileSize parameter, similar to the one used for Ortho Producers (It should be the same, but can be changed depending on the amount of details that the user wants to be displayed at each level).
Those Curves are then split in segments which are stored in a Grid covering the whole tile. Note that each Bank Curves will always be in the same grid cells as their corresponding river axis, and vice-versa. This allows to quickly retrieve the closests distances to each bank at a given point. This is guaranteed by the fact that we add a radius factor around each segment, and add the segment to each cell that are inside this radius. The radius depends on the largest river contained in the tile.
When computing the velocity field at a given point, we must first check if the point is inside a river. If it is, the velocity at that point will be the derivative of the finite differences of the interpolated values of 4 points around the current point.
To determine if a point is inside a river, we browse every river axis stored in the grid cell corresponding to the current point, if any. For each river axis, we just need to determine the distance from the point to the closest curve segment. If it is large than the river's radius, we may already exclude the river from the potential value computation. For each remaining rivers, we get the corresponding banks, and compute the signed distances to each of them. If a signed distance is negative, this means that the point if outside that bank. If a river axis doesn't have at least two corresponding banks with positive distances, the point will be considered outside the river, and the banks will be ignored too. The resulting value is an interpolation of the remaining banks potential values, if any.
The links between river axis and river bank is used to ensure that we don't use unnecessary banks or rivers in the interpolation, which would both slow down the algorithm and bias the computation.
Finally, to improve even more the computation speed, we added an array that stores the computed velocities at each pixel in the tile, so we can reuse it when we need a velocity at a close point. Since the velocity is the derivative of four values, we always check if we have any of them before starting the computation. Indeed, if one of them is negative, the point is outside the river, and thus, we don't have to re-do the whole process. The size of that grid depends on the potentialDelta parameter in the HydroFlowProducer class and also on the level of the current tile. That potentialDelta is a ratio applied to the current tile size to determine the size of the cache. It will be at most the same size as the displayTileSize parameter, i.e. the displayed tiles (same as before, this should be equal to the tileSize parameter of the Ortho producers). That parameter is used when only a few details are required (far point of view) and that we don't need to use as much memory as for when the camera is close to the ground. It is associated to the displayed level to avoid discontinuities in velocities (interpolation distances would not be the same, and thus, at level n, it would display a speed twice faster as the one in level n - 1). The default value is 0.01. The same criteria is used to determine if we need to create a new Flowtile or not: At some point, two successive levels would only contain the same amount of details, and then, we would use unnecessary memory. We can determine the level at which this happens, and only use the parent tile when needed.
Implementation
The above algorithm and the acceleration data structures used to speed up computations are implemented in the proland::HydroFlowTile class. An instance of this class contains the acceleration data structures for the clipped graph corresponding to a terrain tile (the clipped graph is not stored in the hydro flow tile itself but in the tile cache associated with the proland::GraphProducer of the hydro graph). Its role is to test if a given point is inside a river or not and, if yes, to compute the river velocity at this point.
These hydro flow tiles are produced by a proland::HydroFlowProducer, from the hydro graph tiles produced by a proland::GraphProducer (supposed to produce graphs whose curves are instances of proland::HydroCurve).
- Note:
- In addition to being a proland::TileProducer, a proland::HydroFlowProducer is also a proland::CurveDataFactory. This is not needed for computing the river velocity field, but only for the rendering step (see next sections).
A proland::HydroFlowProducer can be loaded with the Ork resource framework, using the following format:
<hydroFlowProducer name="myFlow1" cache="anObjectTileCache" graphs="myRiverGraph"
displayTileSize="192" slip="0.9" searchRadiusFactor="20" potentialDelta="0.01"/>
- The
cacheattribute is the TileCache that stores the tiles produced by this producer. It should be linked to an ObjectTileStorage. - The
graphsattribute is the GraphProducer used to create an HydroGraph. An assertion will occur if the Graphs provided are not HydroGraph or LazyHydroGraph (or derived). - The
displayTileSizeattribute is the size of a displayed tile. It should be the same as on the Ortho GPU tiles. - The
slipattribute determines slip conditions at boundaries (see Qizhi Yu's paper for details). - The
searchRadiusFactorattribute determines the radius of a search region for finding the river banks whose potentials must be interpolated at a given point (see previous paragraph). - And finally, the
potentialDeltaattribute determines the position of the points used to interpolate the velocity, as well as the size of the velocity cache. (See previous paragraph).
In order to be able replace Qizhi Yu's procedural velocity field algorithm with other algorithms, possibly not based on graphs at all, we provide an abstract proland::particles::FlowTile interface, which is implemented by proland::HydroFlowTile. The main functions of this interface are getType and getVelocity, which both take as input a 2D coord, and produce a DATATYPE and a velocity in output (only for the second method). The particle producer (see next section) uses this interface instead of the concrete proland::HydroFlowTile implementation, in order to be able to replace it with another implementation.
In order to represent the motion of fluid-like systems, a well known technique consists in using Particles. Particles are in fact just the representation of an object by using a single position (2D or 3D, depending on what we need to do), and possibly a few more attributes to determine its behavior. Generally, we need them to be created, updated and deleted when they are no longer usefull. They are generally used to simplify the handling of large number of similar objects.
As said before, in Qizhi Yu's algorithm, particles are first generated in screen space and then advected in world space. Their screen coordinates must then be updated to be consistent with their world coordinates. Particles generation is based on a Poisson-disk distribution in screen space, and this distribution must be checked and ensured at each frame, by adding or removing particles wherever it is required. Particles also have a maximum life length, plus a fade in and a fade out states, to avoid popping effects when they disappear.
The algorithm is the following one (called at each frame) :
- World space advection of the particles : Update the particles world coordinates depending on the rivers we have
- Computing the new screen space coordinates
- Checking if some particles must be destroyed, either because they are too close to other, or if they are too old
- Adding new particles if there are holes in the poisson-disk distribution
- Computing the world space coordinates of the newly added particles
Implementation
Proland provides all the required tool for using particles:
First, we have a proland::ParticleStorage, a proland::ParticleStorage::Particle cache able to create and delete particles at will, without calling new / delete methods (it allocates memory at the begining of the program depending on the content that particles will have to contain). This ParticleStorage is used by a proland::ParticleProducer, which then handles the particles. It has a list of proland::ParticleLayer, each dedicated to a given task, and calls for each of them the three following methods:
- proland::ParticleLayer::moveParticles: This should update the coordinates of the particles in every spaces.
- proland::ParticleLayer::removeOldParticles: Since every particle has a lifespan, it is supposed to die at some point. This is where this happens, and this allows to add special behavior when this happens for each layer.
- proland::ParticleLayer::addNewParticles: used for newly added particles.
Every layer then adds the content it needs to particles. For that, is must contain a structure with the elements it needs. The ParticleProducer will then be able to determine the amount of memory space required for each Particle via the proland::ParticleLayer::getParticleSize method. Each layer is then able to convert a Particle to a specialized Particle class containing the specific data for this layer.
A few predefined layers are provided:
- LifeCycleParticleLayer : Handles the particles life cycle: It stores every particles time of birth, and is then able to determine their intensity. It is also able to determine if a particle is fading in or out via this time of birth.
- ScreenParticleLayer : Creates the particles in screen space with a poisson-disk distribution. It also contains, for each particle, their screen space coordinates and a reason parameter, used to determine why the ScreenParticleLayer has killed a particle (only used if the particle is currently fading out). It also transforms the particles coordinates from screen space to world space, using a SceneManager as reference. In order to store and quickly access particles, the ScreenParticleLayer uses a proland::ParticleGrid. The window is divided into a regular grid, and each cell of that grid contains the particles covering it. This allows to quickly retrieve the neighbors of a given particle for example, and also to accelerate the GPU rendering of particles (see next section).
- WorldParticleLayer : Adds for each particle world space 3D coordinates as well as a world velocity. At each moveParticles call, it updates the coordinates of each particle depending on the content of their velocity data. It also has a paused status, that enables to pause the particles update.
- TerrainParticleLayer : This layer stores a list of SceneNodes, and is able to determine on which one a Particle is. It also stores terrain space coordinates and a status for each particles. At moveParticles call, it updates the particles coordinates depending on the content of the FlowTiles created on the TerrainNode. (That TerrainNode must have a TileProducer that produces FlowTiles). It also updates the world velocity of the moving particles.
- RandomParticleLayer : just contains a random 3D vector contained in given bounds for each particles.
Particles are also compatible with GLSL shaders: The ParticleProducer is able to convert the particles data into a format usable in GPU glsl shaders. This is done through the the ParticleProducer#copyToTexture method. That method takes as input an ork::TextureRectangle and a callback function witch will determine what content will be set in the texture. The result is then contained in the provided texture. The particles are ordered depending on their position in the ParticleStorage memory space.
proland::ParticleGrid is also able to convert its data to a format usable in GPU glsl shaders, also through its copyToTexture method. This one copies the indices of each particle in the texture provided as input. A maximum amount of particles for each cell can be determined, because browsing too much particles for each pixel can be very time consuming. This texture will then work as an indirection table, and it will be fairly simple to retrieve what particles cover a given pixel thanks to it.
The Particle framework can be loaded in the ork resource framework:
First, we need a ParticleStorage to store the particles.
<particleStorage name="particleStorage1" capacity="5000" pack="true"/>
The available parameters are the following ones:
capacity: the maximum amount of particles that this storage can create.pack: determines how the particles will be organized in the memory space. If true, Creating and deleting particles will be longer, but the time used to access to them will be reduced and every particle will be contiguous in memory.
Then, we can create the ParticleProducer and all of its layers inside it:
<particleProducer name="particles1" storage="particleStorage1">
<terrainParticleLayer name="terrainLayer" terrains="terrainNode1/riverFlow,terrainNode2/riverFlow"/>
<worldParticleLayer name="worldLayer" speedFactor="1.0"/>
<screenParticleLayer name="screenLayer" radius="30"/>
<lifeCycleParticleLayer name="lifeLayer" fadeInDelay="5" fadeOutDelay="0.5" activeDelay="30" unit="s"/>
<randomParticleLayer name="randomLayer" xmin="-1" ymin="-1" zmin="-1"/>
</particleProducer>
The ParticleProducer only takes one parameter: the storage. Then, it may have a unlimited number of child nodes corresponding to its ParticleLayers. A few examples are given here:
- TerrainParticleLayer: its input parameters are a list of
terrainsorganized as such : first, it needs the TerrainNode containing a TileProducer that produces FlowTiles. then, separated by a slash, it reads the name of that TileProducer in the TerrainNode. If the Scene contains multiple terrains, they must be separated by a coma. - WorldParticleLayer: contains the
speedFactorof every displacement of particles, in world space. - ScreenParticleLayer: needs the
radiusof every generated particles, in screen space. - LifeCycleParticleLayer: the life cycle delays can be specified: the
fadeInDelayandfadeOutDelayare used for blending in/out the particle. TheactiveDelayparameter defines the lifespan of the particle. The unit for these parameters is in seconds by default, but can be changed via theunitparameter (can be s(seconds), ms(milliseconds) or us (microseconds). - RandomParticleLayer: The user can specify the
xmin,xmax,ymin,ymax,zminandzmaxboundary values of the randomly generated coordinates. Default are [0-1] for each dimension.
We will now focus on the rendering part.
We now have particles that fully cover the screen space, and are able to advect them. Each particle is associated to a Sprite containing a texture. That texture is in fact a random portion of a larger texture containing wave-like normals. To make the rivers less stationary, especially for lakes, where there is no flow, this texture can be updated through time.
Then, we only have to blend and render those sprites in an efficient way. For that, we rely on the indirection grid presented in the previous section (ParticleGrid content). That grid contains only the indices of each Particle covering a given cell, to avoid redundancy. The parameters of each particle are then stored in a different texture (see ParticleProducer in previous section). The parameters are the following ones:
- Screen space coordinates
- World space woordinates
- Random Texture coordinates
- Particle Intensity
- Particle Radius, in screen space
The algorithm is then the following one: For every pixels, we access the indirection grid to find all the sprites covering the current pixel. For each sprite, we read its parameters from the parameters texture. We then compute the contribution of each sprite and blend the result depending on the distances to each sprite, their intensity, etc...
The equation used to determine the contribution of a sprite is the following one:
where i is the index of the sprite, T is a wave texture, pi is the coordinates of the sprite in world space, and ui is a random texture coordinates, constant through the whole life of the sprite.
The equation to compute the final result is the following one:
Where the weighting factor wi depends on the distance to the center of the sprite and the intensity of the sprite. Since the intensity depends on the life cycle of the particles (which makes them fading in and out), we won't have popping effects when sprites are deleted.
We can then apply ordinary shaders : bump mapping, refraction and reflection, shading...
An other point we had to focus on was how to draw the rivers in an efficient way: Indeed, we couldn't just draw every graph from every visible tiles as we do in GraphLayers: this would take too much time to redraw at each frame (we would have more than a few thousands vertices when zooming in, even for small graphs, especially for flattened graphs). Instead of that, we decided to browse each displayed tiles and to store which curves should be displayed. We also sort out the Curves that are too small to be drawn (width inferior to 1 pixel on screen). Then, we browse every area containing those curves, and give them as input to a Tesselator, which directly computes the resulting mesh. Finally, we store that mesh so we won't have to recompute it at each frame, but only to call the draw method. Then, for each vertex, we access the elevation table to determine the elevation of the ground, so the river can be drawn directly on the terrain.
Nevertheless, this method has drawbacks and creates artefacts if the elevation is not constant and if the rivers are too large: the Tesselator can create very long and thin triangles, and if the elevations are too much different from one point of the triangle to another, this will create the visual bugs seen in the next image. Adding an Elevation layer on the terrain can help to reduce that effect.
Implementation
In the Ork resource framework, Rivers are simply a node. It has flags "Object" and "Dynamic", in order to use the framework ability to build the taskgraph at each frame before actually doing the task.
In our case, the updateMethod call uses the proland::UpdateRiversTask Task class, a Task that asserts that every required resource is available. The drawMethod call uses the proland::DrawRiversTask Task class, which updates the particles and call the texture advection method for drawing rivers. Note that only the drawing part is done on GPU.
The UpdateRiversTask task checks, at each frame, if new Tiles are displayed. If that's the case, it is requested to the producers, and the tiles that are not longer visible are released. It also checks if the tiles were changed since last frame, in which case they must be updated (and so does the TaskGraph). It handles the Flow Producer and the river Graph Producer used by a given ParticleProducer. It also forces the creation of a TileMap for normal and elevation tiles. This TileMap will enable us to quickly retrieve the elevations and normals at a given terrain space coordinate directly in the GPU, without fetching it to the CPU at all. TileMaps are explained in the terrain framework section.
The DrawRiversTask task then uses the data from every visible tiles to draw the rivers. First, it updates the Particles (ParticleProducer#updateParticles), and the gpu structures as well. Then, depending on some internal parameters, it will display:
-
The Rivers. Different display types are available:
- Nothing,
- Mesh only,
- Advected Normals,
- Non Advected Normals(a simple texture is applied),
- Particle Coverage,
- SpriteGrid display.
- The Particles,
- The Velocities,
- The sun effects, provided by the ocean framework,
- A Fog effect (to reduce glowing effects, which are still here despite the mip-mapping).
To draw rivers, we use the same display method as in GraphLayers: Large rivers (those we want to draw) are represented as areas. As explained before, we don't draw every curve, and only draw each curve at most once. For each SceneNode, we apply the method described above, and only recompute it when a new tile appears on screen, or when a tile is updated (either flow or graph). This enables us to easily have real-time editable rivers.
To draw the rivers, we moslty rely on a bump-mapping method, which uses the result of the blending equation described above (F function). We treat the result of that function as the new normals, and use them in the bump-mapping part.
The wave textures are called proland::WaveTile objects. They contain a 2D Texture, which can be updated through time through the timeStep method.
3 implementations are provided:
- WaveTile: This first one just takes in parameter a Texture2D, and uses it without modifying it. It will be the same during the entire execution.
- PerlinWaveTile: This WaveTile generates a single Perlin Noise texture at launch, and uses it like a WaveTile.
- AnimatedPerlinWaveTile: Creates N PerlinWaveTiles and alternates between all of them regularily in time. This creates a flow sensation even if particles are not moving.

All these objects can be loaded in the Ork resource framework:
-
WaveTile:
<animatedWaveTile name="myWaveTile1" texture="mytexture" tileSize=1 gridSize=256 waveScale=1.0 timeLoop=32/>
These are the default values. The following parameters are the same for the 3 presented WaveTile Objects, but not all of them are used in the base classes.
tex: the Texture2D that contains the wave profiles. only used for WaveTile.gridSize: size of the texture.tileSize: size of a tile.waveScale: size of a wave.timeLoop: number of frames of a wave cycle.
-
UpdateRiversTask:
<updateRiversTask name="myUpdateTask" particles="myRiverParticleManager" timeStep=1/>
particlesa ParticleProducer.timeSteptime step at each frame. Changes the speed of the river.
-
DrawRiversTask:
<drawRiversTask name="myDrawRiversTask" particles="myRiverParticleManager" drawParticles="true" particleRadius=0.01 timeStep=1 texture="myWaveTile1" fogStart=0 fogEnd=5/>
These are the default values.
particles: the ParticleProducer used to create the flow.timeStep: time step at each frame. Changes the speed of the river.drawGrid: determines whether we draw the screen sprite grid or not. Mainly used for debug.drawParticles: determines whether we draw the particles or not. Particles are drawn as colored dots.texture: the texture used to advect normals.fogStart and fogEnd: fog distances (x: closest, y: furthest).
